基于马尔可夫链蒙特卡罗模拟的权证定价方法研究
硕士学位论文I摘要权证市场作为我国资本市场的重要组成部分,近年来得到了快速发展,权证定价问题也得到了深入的研究,其中的波动率研究是最重要的一部分。在证实金融资产价格波动率具有尖峰肥尾、群集效应、杠杆效应和长记忆等时变特性的研究成果不断出现的背景下,以常数波动率为假设的Black-Scholes期权定价理论已经远远无法满足更精细的金融实务操作的要求了。研究波动率时变性的模型可以分为ARCH/GARCH模型和随机波动率模型两大类。从理论上,随机波动率模型要优于ARCH/GARCH模型,但由于前者的估计方法较复杂而没有如后者那样在实际中受到广泛应用。近年来,针对随机波动率模型参数估计方法的研究已经成...
相关推荐
-
建筑工程投标文件范本-(格式)VIP免费

 2024-11-22 48
2024-11-22 48 -
疾病预防控制中心招标文件VIP免费

 2025-01-09 50
2025-01-09 50 -
体育健身中心施工招标文件VIP免费

 2025-01-09 32
2025-01-09 32 -
江西丰城电厂及广东从化事故案例分析VIP免费

 2025-03-04 7
2025-03-04 7 -
钢结构节点图集CAD版(可编辑)VIP免费

 2025-03-04 20
2025-03-04 20 -
[青岛]精品工程亮点做法图片集(130页)VIP免费

 2025-03-04 13
2025-03-04 13 -
外墙外保温工程技术规程JGJ144-2019VIP免费

 2025-03-04 11
2025-03-04 11 -
地铁停车场施工组织设计VIP免费

 2025-03-04 14
2025-03-04 14 -
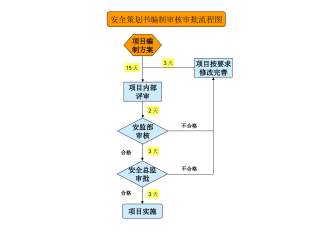
项目建设安全管理流程图汇编VIP免费
 2025-03-04 34
2025-03-04 34 -
特训班学习心得VIP免费

 2025-03-04 10
2025-03-04 10
相关内容
-

[青岛]精品工程亮点做法图片集(130页)
分类:行业资料
时间:2025-03-04
标签:建筑工程、精品工程、细部节点做法、亮点做法
格式:PPT
价格:5 积分
-

外墙外保温工程技术规程JGJ144-2019
分类:行业资料
时间:2025-03-04
标签:外墙保温、工程、规范
格式:ZIP
价格:2 积分
-

地铁停车场施工组织设计
分类:行业资料
时间:2025-03-04
标签:地铁、场段、施工组织设计
格式:DOCX
价格:3 积分
-

项目建设安全管理流程图汇编
分类:行业资料
时间:2025-03-04
标签:安全管理、流程图
格式:PPT
价格:1 积分
-

特训班学习心得
分类:行业资料
时间:2025-03-04
标签:拓展培训、结构化思考、培训、心得体会
格式:DOCX
价格:1 积分






