基于数值降维技术的期权组合非线性VaR模型的研究
硕士学位论文I摘要随着全球金融市场的快速发展,各种金融衍生产品涌流而成,金融衍生产品市场得到了迅猛发展。金融衍生产品能够实现套期保值、风险管理、价值定位等一系列功能。然而,在进行风险规避的同时,由于自身高杠杆、低交易成本、流动性强等特点,金融衍生产品产生了新的金融风险。另一方面,作为一种初级金融衍生产品的权证已于2005年7月在沪深两市重新开始了交易。经过四年的发展,两市权证交易量已初具规模。2007年,沪深两市总成交量已超过6.97万亿元。与此相对应,对权证交易进行合理有效的风险测度成为了一个现实的问题。VaR方法是一种各国普遍采用的风险管理方法,具有全面性、简明性和实用性等特点,符合金融机...
相关推荐
-
建筑工程投标文件范本-(格式)VIP免费

 2024-11-22 48
2024-11-22 48 -
疾病预防控制中心招标文件VIP免费

 2025-01-09 50
2025-01-09 50 -
体育健身中心施工招标文件VIP免费

 2025-01-09 32
2025-01-09 32 -
江西丰城电厂及广东从化事故案例分析VIP免费

 2025-03-04 7
2025-03-04 7 -
钢结构节点图集CAD版(可编辑)VIP免费

 2025-03-04 20
2025-03-04 20 -
[青岛]精品工程亮点做法图片集(130页)VIP免费

 2025-03-04 13
2025-03-04 13 -
外墙外保温工程技术规程JGJ144-2019VIP免费

 2025-03-04 11
2025-03-04 11 -
地铁停车场施工组织设计VIP免费

 2025-03-04 14
2025-03-04 14 -
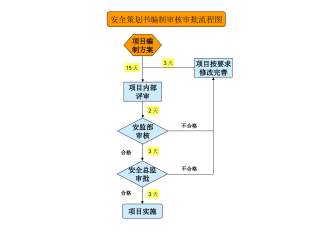
项目建设安全管理流程图汇编VIP免费
 2025-03-04 34
2025-03-04 34 -
特训班学习心得VIP免费

 2025-03-04 10
2025-03-04 10
相关内容
-

[青岛]精品工程亮点做法图片集(130页)
分类:行业资料
时间:2025-03-04
标签:建筑工程、精品工程、细部节点做法、亮点做法
格式:PPT
价格:5 积分
-

外墙外保温工程技术规程JGJ144-2019
分类:行业资料
时间:2025-03-04
标签:外墙保温、工程、规范
格式:ZIP
价格:2 积分
-

地铁停车场施工组织设计
分类:行业资料
时间:2025-03-04
标签:地铁、场段、施工组织设计
格式:DOCX
价格:3 积分
-

项目建设安全管理流程图汇编
分类:行业资料
时间:2025-03-04
标签:安全管理、流程图
格式:PPT
价格:1 积分
-

特训班学习心得
分类:行业资料
时间:2025-03-04
标签:拓展培训、结构化思考、培训、心得体会
格式:DOCX
价格:1 积分






