双指数跳扩散模型期权的最小风险定价及参数估计
硕士学位论文I摘要Black-Scholes模型在期权定价领域获得了前所未有的成功,但是模型无法解释标的资产收益的一些己知统计特征,如尖峰、波动集聚和长记忆性。众多的学者通过对Black-Scholes研究成果提出许多拓展的模型,从而达到了更好地描述资产收益分布的经验特征。实证研究表明股票收益的变化具有跳跃性。一个合理的解释是,股票收益率是一个跳跃扩散过程,于是对Black-Scholes模型进行修正,加入跳跃项。实证分析证实,这类模型可在某些情形下克服隐含波动率的“微笑”与“偏差”效应,且根据该模型得到的欧式期权定价与市场价格吻合程度更好。S.G.Kou提出的双指数跳扩散模型便是其中的一种,...
相关推荐
-
建筑工程投标文件范本-(格式)VIP免费

 2024-11-22 48
2024-11-22 48 -
疾病预防控制中心招标文件VIP免费

 2025-01-09 50
2025-01-09 50 -
体育健身中心施工招标文件VIP免费

 2025-01-09 32
2025-01-09 32 -
江西丰城电厂及广东从化事故案例分析VIP免费

 2025-03-04 7
2025-03-04 7 -
钢结构节点图集CAD版(可编辑)VIP免费

 2025-03-04 20
2025-03-04 20 -
[青岛]精品工程亮点做法图片集(130页)VIP免费

 2025-03-04 12
2025-03-04 12 -
外墙外保温工程技术规程JGJ144-2019VIP免费

 2025-03-04 11
2025-03-04 11 -
地铁停车场施工组织设计VIP免费

 2025-03-04 14
2025-03-04 14 -
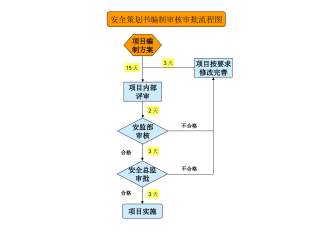
项目建设安全管理流程图汇编VIP免费
 2025-03-04 34
2025-03-04 34 -
特训班学习心得VIP免费

 2025-03-04 10
2025-03-04 10
相关内容
-

[青岛]精品工程亮点做法图片集(130页)
分类:行业资料
时间:2025-03-04
标签:建筑工程、精品工程、细部节点做法、亮点做法
格式:PPT
价格:5 积分
-

外墙外保温工程技术规程JGJ144-2019
分类:行业资料
时间:2025-03-04
标签:外墙保温、工程、规范
格式:ZIP
价格:2 积分
-

地铁停车场施工组织设计
分类:行业资料
时间:2025-03-04
标签:地铁、场段、施工组织设计
格式:DOCX
价格:3 积分
-

项目建设安全管理流程图汇编
分类:行业资料
时间:2025-03-04
标签:安全管理、流程图
格式:PPT
价格:1 积分
-

特训班学习心得
分类:行业资料
时间:2025-03-04
标签:拓展培训、结构化思考、培训、心得体会
格式:DOCX
价格:1 积分






